Create the Union of Grid instances

import matplotlib.pyplot as plt
import minterpy as mp
import numpy as np

This guide demonstrates how to take the union of instances of Grid and the expected outcome of such an operation. The union between two instances of Grid may be obtained via the operator |.

The union between two instances of Grid is another instance of Grid whose underlying multi-index set is the union of the index sets of the operands. This Grid instance can support interpolation polynomials that are the summed of polynomials that live on either Grid operands.

To know more about the multi-index set union in Minterpy, see the relevant example.

When taking the union of two instances of Grid note the following caveats:

• If a generating function is defined in both instances, then the instances can be multiplied only if the generating functions are compatible, i.e., they are the same function. defined in both instances.

• Without a generating function, two instances can be multiplied only if the generating points are compatible, i.e., they have the same values up to a common dimension (or columns).

Example: Instances with the same dimension

As a motivating example, consider two two-dimensional interpolation grids:

• The first grid has the multi-index set \(\{(0, 0), (1, 0), (0, 1), (1, 1), (0, 2), (1, 2) \}\) with respect to \(l_p\)-degree \(2.0\)

• the second grid has a complete multi-index set with respect to a polynomial degree \(2\) and \(l_p\)-degree \(\infty\).

Both interpolation grids have points according to the Leja-ordered Chebyshev-Lobatto points (the default in Minterpy).

First, create the instances of Grid according to the above specification:

mi_1 = mp.MultiIndexSet(
    np.array([[0, 0], [1, 0], [0, 1], [1, 1], [0, 2], [0, 3]]),
    lp_degree=2.0,
)
grd_1 = mp.Grid(mi_1)
grd_2 = mp.Grid.from_degree(2, 2, np.inf)

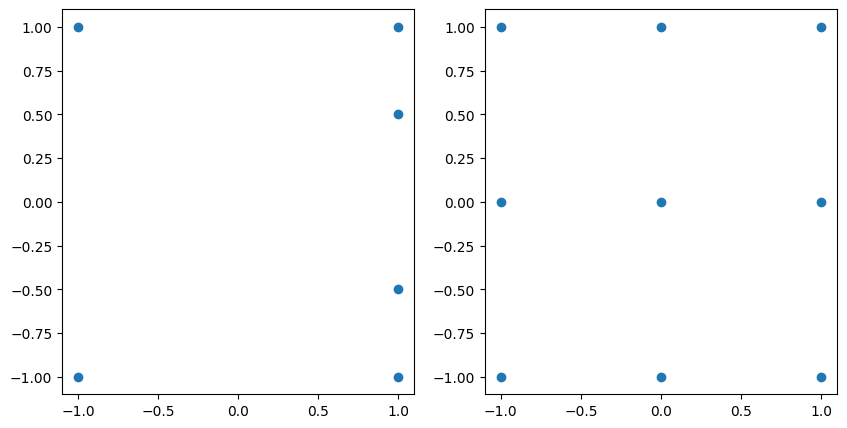
The unisolvent nodes that correspond to these grids are shown below:

fig, axs = plt.subplots(1, 2, figsize=(10, 5))
axs[0].scatter(grd_1.unisolvent_nodes[:, 0], grd_1.unisolvent_nodes[:, 1])
axs[1].scatter(grd_2.unisolvent_nodes[:, 0], grd_2.unisolvent_nodes[:, 1]);

The union Grid can be obtained as follows:

grd_union = grd_1 | grd_2

And the resulting unisolvent nodes are shown below:

plt.scatter(grd_union.unisolvent_nodes[:, 0], grd_union.unisolvent_nodes[:, 1]);

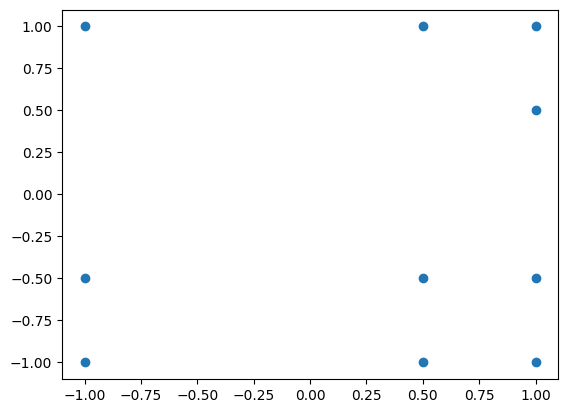
Notice that the underlying multi-index set follows the convention adopted for the union of MultiIndexSet:

print(grd_union.multi_index)

MultiIndexSet(m=2, n=3, p=inf)
[[0 0]
 [1 0]
 [2 0]
 [0 1]
 [1 1]
 [2 1]
 [0 2]
 [1 2]
 [2 2]
 [0 3]]

Example: Instances with different dimension

Union of grids of different spatial dimensions may also be obtained. For instance, consider the product of two interpolation grids:

• the first grid is a one-dimensional grid whose a complete multi-index set with respect to a polynomial degree \(4\)

• the second grid is a two-dimensional grid whose a complete multi-index set with respect to a polynomial degree \(2\) and \(l_p\)-degree \(1.0\).

Both interpolation grids have points according to the Leja-ordered Chebyshev-Lobatto points (the default in Minterpy).

The product grid will have the same spatial dimension as that of the operands with the largest dimension.

First, create the two instances of Grid following the above specification:

grd_1 = mp.Grid.from_degree(1, 4, 1.0)
grd_2 = mp.Grid.from_degree(2, 2, 1.0)

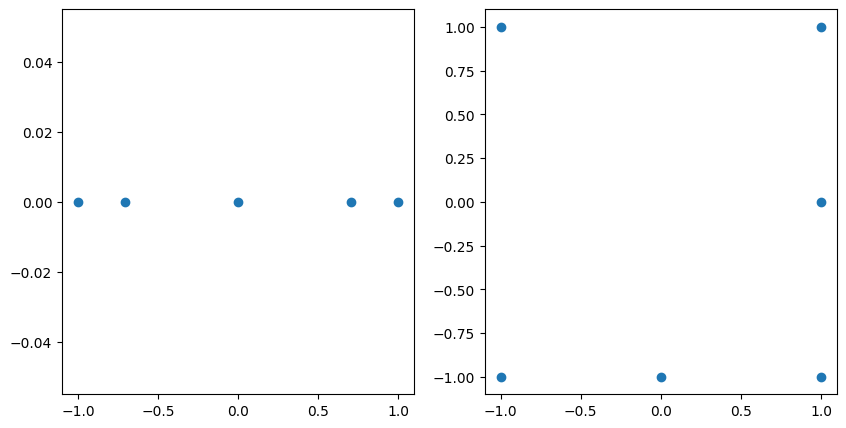
The unisolvent nodes that correspond to these are shown below:

fig, axs = plt.subplots(1, 2, figsize=(10, 5))
axs[0].scatter(grd_1.unisolvent_nodes[:, 0], np.zeros(len(grd_1.multi_index)))
axs[1].scatter(grd_2.unisolvent_nodes[:, 0], grd_2.unisolvent_nodes[:, 1]);

The union Grid can be obtained as follows:

grd_union = grd_1 | grd_2

And the resulting unisolvent nodes are shown below:

plt.scatter(grd_union.unisolvent_nodes[:, 0], grd_union.unisolvent_nodes[:, 1]);

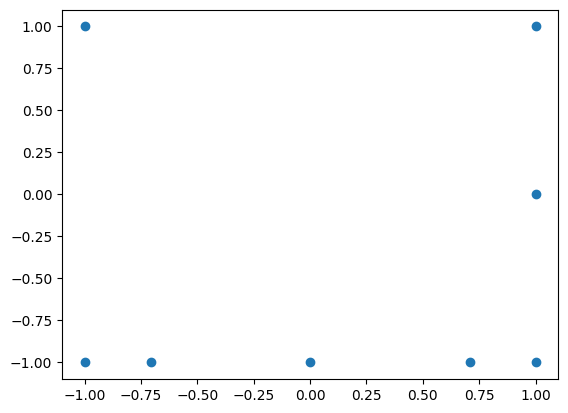
As expected the resulting Grid is two-dimensional according to the largest dimension of the operands. The resulting multi-index set is shown below:

print(grd_union.multi_index)

MultiIndexSet(m=2, n=4, p=1.0)
[[0 0]
 [1 0]
 [2 0]
 [3 0]
 [4 0]
 [0 1]
 [1 1]
 [0 2]]