Create a Grid from an Array of Generating Values#
import numpy as np
import minterpy as mp
import matplotlib.pyplot as plt
Minterpy interpolating polynomials (i.e., in the Lagrange or Newton basis) lives on a grid that holds the so-called unisolvent nodes. An interpolating multi-dimensional polynomial of a given multi-index set of exponents is uniquely determined on the corresponding unisolvent nodes.
An instance of Grid can be constructed via different constructors:
Grid.from_value_set(): create an instance based on an array of generating values (this page)Grid.from_function(): create an instance with a generating function (see the example)Grid.from_points(): create an instance with an array of generating points (see the example)Grid.from_degree(): create an instance with a complete multi-index set (see the example)
This guide provides an example on how to construct a Grid instance based
on a given array of generating values (i.e., one-dimensional interpolation
points) using the from_value_set() method.
About generating values#
Generating values in Minterpy convention, are one-dimensional interpolation points. When used to define a grid to support multi-dimensional polynomials, the generating values will be converted to an array of generating points via tiling procedure.
Valid generating values to create an instance of Grid are given as
a one-dimensional array of floats that must additionally satisfy the following
conditions:
the length must be \(n + 1\) where \(n\) is the maximum polynomial degree across all dimensions that the grid must support.
the values of the array must be unique, that is, it contains no repeats.
the length must be equal to or larger than the maximum exponents of the grid’s multi-index set in any dimension.
Note
Generating values may also be provided as a two-dimensional array as long as the array only has either one colum or one row.
About the from_value_set() factory method#
The method from_value_set() of the Grid class returns an instance of Grid
based on a given generating values.
The method accepts two mandatory arguments, namely, the multi-index set of exponents that defines the polynomials that grid can support, and the generating values as required by the multi-index set.
As explained above, the array of generating values must satisfy several conditions for it to be valid.
In many applications, a single set of one-dimensional interpolation points
is used for different dimensions.
The from_value_set() method is a shortcut to create a grid with
a specific one-dimensional interpolation points that are replicated
in every dimension.
Example: Two-dimensional interpolation grid#
Create an interpolation grid in \([-1, 1]^2\) to support two-dimensional polynomials having a multi-index set \(A = \{ (0, 0), (1, 0), (2, 0), (0, 1), (1, 1), (2, 1), (0, 2), (1, 2), (2, 2), (0, 3) \}\) (defined with respect to \(l_p\)-degree \(1.0\)). The interpolation grid has Leja points in every dimension.
Multi-index set#
Create an instance of MultiIndexSet following the above specification:
exponents = np.array([
[0, 0],
[1, 0],
[2, 0],
[0, 1],
[1, 1],
[2, 1],
[0, 2],
[1, 2],
[2, 2],
[0, 3],
])
mi = mp.MultiIndexSet(exponents, lp_degree=1.0)
print(mi)
MultiIndexSet(m=2, n=4, p=1.0)
[[0 0]
[1 0]
[2 0]
[0 1]
[1 1]
[2 1]
[0 2]
[1 2]
[2 2]
[0 3]]
Generating values#
The required generating values as required by the grid are given as follows:
gen_values = np.array([0, -1, 1, 0.57735035])
Because the maximum exponents in the multi-indices across all dimensions is \(3\), the required number of generating values is \(3 + 1 = 4\).
Grid instance#
An instance of Grid given the multi-index set and the array of generating values
can be constructed via from_value_set() method as follows:
grd = mp.Grid.from_value_set(mi, gen_values)
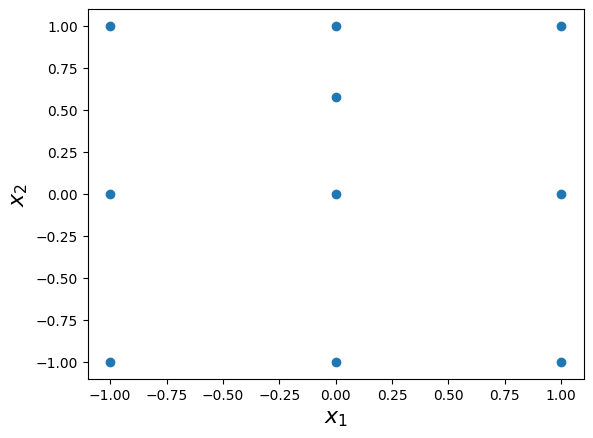
The grid has the following unisolvent nodes:
print(grd.unisolvent_nodes)
[[-0. 0. ]
[ 1. 0. ]
[-1. 0. ]
[-0. -1. ]
[ 1. -1. ]
[-1. -1. ]
[-0. 1. ]
[ 1. 1. ]
[-1. 1. ]
[-0. 0.57735035]]
The two-dimensional interpolation grid is plotted below:
plt.scatter(grd.unisolvent_nodes[:, 0], grd.unisolvent_nodes[:, 1])
plt.xlabel("$x_1$", fontsize=16)
plt.ylabel("$x_2$", fontsize=16);