Make a Grid Complete#

import minterpy as mp
import numpy as np
import matplotlib.pyplot as plt

A Grid instance is defined by a multi-index set which itself may or may not be complete (see Make a Multi-Index Set Complete for more details) A Grid is therefore complete if the underlying multi-index set is complete; it is incomplete otherwise. This guide shows how to check if a given Grid instance is complete and make it complete.

Motivating example#

Consider a two-dimensional Leja-ordered Chebyshev-Lobatto interpolation grid whose underlying multi-index set contains the elements:

A = {(1, 0), (0, 2)}

with respect to $l_{p}$ -degree of $2.0$ .

This grid is incomplete; make the grid complete and plot the corresponding unisolvent nodes.

The multi-index set of the Gridcan be created in Minterpy as follows:

mi = mp.MultiIndexSet(np.array([[1, 0], [0, 2]]), lp_degree=2.0)

print(mi)

MultiIndexSet(m=2, n=2, p=2.0)
[[1 0]
 [0 2]]

This set has a polynomial degree of:

mi.poly_degree

Note

This polynomial degree corresponds to the minimum degree $n$ such that all elements in the multi-index set satisfy the $l_{p}$ -norm condition $‖ α ‖_{p} = (α_{1}^{p} + \dots + α_{m}^{p})^{\frac{1}{p}} \leq n$ for all $α \in A$ . Given a set of exponents and $l_{p}$ -degree, Minterpy automatically infers this polynomial degree.

An instance of Grid given the multi-index set can then be created as follows:

grd = mp.Grid(mi)

Note that by default, the underlying generating points are the Leja-ordered Chebyshev-Lobatto points.

Check for completeness#

The property is_complete of a Grid instance returns True if the set of exponents in the instance is complete and False otherwise.

grd.is_complete

False

The check indicates that the given grid is not complete with respect to the given polynomial degree and $l_{p}$ -degree.

Make complete#

The method make_complete() creates a complete Grid whose underlying multi-index set is complete. Calling the method returns a new instance of Grid and the result can be stored in a variable for further use:

The method make_complete() creates a complete multi-index set from a given instance of MultiIndexSet.

grd_complete = grd.make_complete()

Notice that the Grid instance is now complete:

grd_complete.is_complete

True

because the underlying multi-index set is now also complete (with respect to $l_{p}$ -degree $2.0$ ):

grd_complete.multi_index

MultiIndexSet(
  array([[0, 0],
         [1, 0],
         [2, 0],
         [0, 1],
         [1, 1],
         [0, 2]]),
  lp_degree=2.0
)

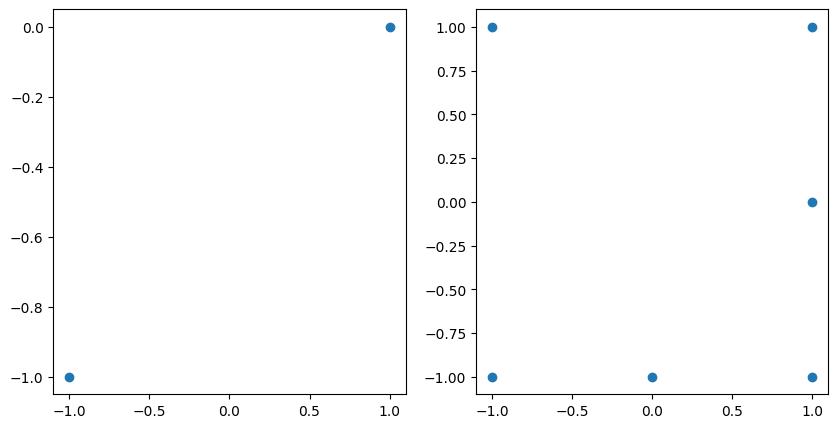
The unisolvent nodes of incomplete and complete grids are shown below:

fig, axs = plt.subplots(1, 2, figsize=(10, 5))
axs[0].scatter(grd.unisolvent_nodes[:, 0], grd.unisolvent_nodes[:, 1])
axs[1].scatter(grd_complete.unisolvent_nodes[:, 0], grd_complete.unisolvent_nodes[:, 1]);

../../_images/7f51ef38a8be32b1ed67c097f79f00aed99e13b56ea6f929fe1396e62e4f0980.png