Basic Arithmetic Operations with Polynomials#
Once you have constructed a polynomial in Minterpy, you can perform various operations on it, depending on the basis in which the polynomial is represented. For instance, as demonstrated in the previous tutorials, you can evaluate a Minterpy polynomial (in the Newton basis) at a set of query points.
This tutorial will show you how to extend beyond evaluation by performing arithmetic operations with Minterpy polynomials. Specifically, you’ll learn that Minterpy polynomials can be:
Added or subtracted from other polynomials
Multiplied by other polynomials or real scalar numbers
Raised to a power (as long as it’s a non-negative integer)
These operations result in another Minterpy polynomial in the same basis. In other words, Minterpy polynomials are closed under the following arithmetic operations:
Multiplying a polynomial by another polynomial
Multiplying a polynomial by a scalar (a real number)
Adding or subtracting one polynomial to/from another
Adding or subtracting a scalar (a real number) to/from a polynomial
Raising a polynomial to a non-negative integer power
To keep things simple, this tutorial uses one-dimensional polynomials as examples. However, the principles and behaviors we’ll cover apply to Minterpy polynomials of any dimensions.
Before you start, make sure to import the necessary packages to follow along with this guide.
import minterpy as mp
import numpy as np
import matplotlib.pyplot as plt
Motivating functions#
Consider the following two one-dimensional functions.
The first is the sine function:
You can define the above function as a lambda function in Python:
fun_1 = lambda xx: np.sin(5 * np.pi * xx)
Following the examples given in the previous guide, you can construct an interpolating polynomial of the function above as follows:
# Multi-index set of polynomial degree 30
mi_1 = mp.MultiIndexSet.from_degree(1, 30)
# Interpolation grid
grd_1 = mp.Grid(mi_1)
# Coefficients of the Lagrange polynomial
coeffs_1 = grd_1(fun_1)
# Lagrange polynomial given grid and coefficients
lag_poly_1 = mp.LagrangePolynomial.from_grid(grd_1, coeffs_1)
# Transformation to the Newton basis
poly_1 = mp.LagrangeToNewton(lag_poly_1)()
You can check the infinity norm of the polynomial to decide if the approximation is good enough.
xx_test = -1 + 2 * np.random.rand(10000)
yy_test_1 = fun_1(xx_test)
yy_poly_1 = poly_1(xx_test)
print(np.max(np.abs(yy_poly_1 - yy_test_1)))
3.9777151428221913e-07
Note
The choice of polynomial degree above is just an example; in practice, you will have to decide what level of accuracy is sufficient for your specific use case. Also, keep in mind that infinity norm is just one way to measure accuracy; other common metrics, like mean-squared error, are also widely used.
The second is the exponential function:
As before, you can define the function as a lambda function:
fun_2 = lambda xx: 2.0 * np.exp(-2.5 * (xx + 1))
and then the interpolating polynomial:
# Multi-index set of polynomial degree 15
mi_2 = mp.MultiIndexSet.from_degree(1, 15)
# Interpolation grid
grd_2 = mp.Grid(mi_2)
# Coefficients of the Lagrange polynomial
coeffs_2 = grd_2(fun_2)
# Lagrange polynomial given grid and coefficients
lag_poly_2 = mp.LagrangePolynomial.from_grid(grd_2, coeffs_2)
# Transformation to the Newton basis
poly_2 = mp.LagrangeToNewton(lag_poly_2)()
Finally, check the infinity norm to decide if the approximation is accurate enough.
yy_test_2 = fun_2(xx_test)
yy_poly_2 = poly_2(xx_test)
print(np.max(np.abs(yy_poly_2 - yy_test_2)))
1.2266854199083355e-12
The plots of both interpolating polynomials are shown below.
Show code cell source
xx_plot = np.linspace(-1, 1, 1000)
fig, axs = plt.subplots(nrows=1, ncols=2, figsize=(10, 4))
axs[0].plot(xx_plot, fun_1(xx_plot), label="true function")
axs[0].plot(xx_plot, poly_1(xx_plot), label="polynomial ($Q$)")
axs[0].scatter(grd_1.unisolvent_nodes[:, 0], coeffs_1)
axs[0].set_xlabel("$x$", fontsize=14);
axs[0].set_ylabel("$f_1(x)$", fontsize=14);
axs[0].set_title("Sine", fontsize=16);
axs[0].tick_params(axis='both', which='major', labelsize=12)
axs[1].plot(xx_plot, fun_2(xx_plot), label="true function ($f$)")
axs[1].plot(xx_plot, poly_2(xx_plot), label="polynomial ($Q$)")
axs[1].scatter(grd_2.unisolvent_nodes[:, 0], coeffs_2, label="interpolating nodes")
axs[1].set_xlabel("$x$", fontsize=14);
axs[1].set_ylabel("$f_2(x)$", fontsize=14);
axs[1].set_title("Exponential", fontsize=16)
axs[1].tick_params(axis='both', which='major', labelsize=12)
axs[1].legend(fontsize=14)
fig.tight_layout()
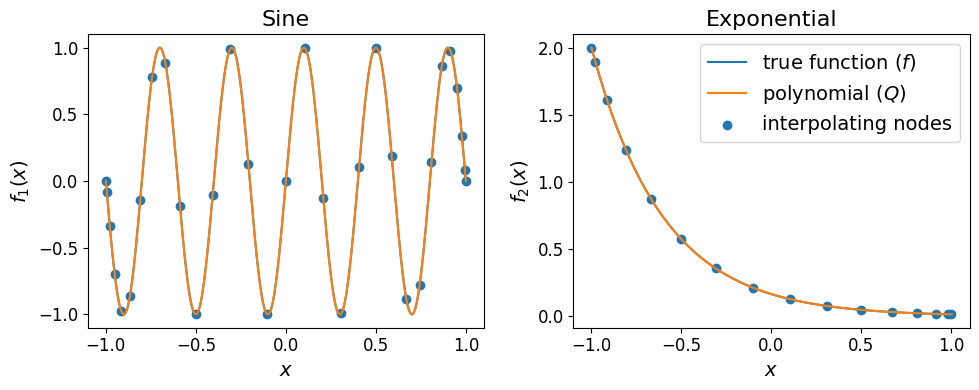
The plots show that there no notable differences between the two true functions and their corresponding interpolating polynomials
Now that you have the two interpolating polynomials, you can start doing arithmetic operations with them.
Addition and subtraction#
Minterpy polynomials may be added or subtracted by a real scalar number; this operation returns another polynomial.
For instance:
poly_scalar_add = poly_1 + 5
poly_scalar_add
<minterpy.polynomials.newton_polynomial.NewtonPolynomial at 0x7febe68475e0>
or:
poly_scalar_sub = poly_1 - 5
poly_scalar_sub
<minterpy.polynomials.newton_polynomial.NewtonPolynomial at 0x7febe68478e0>
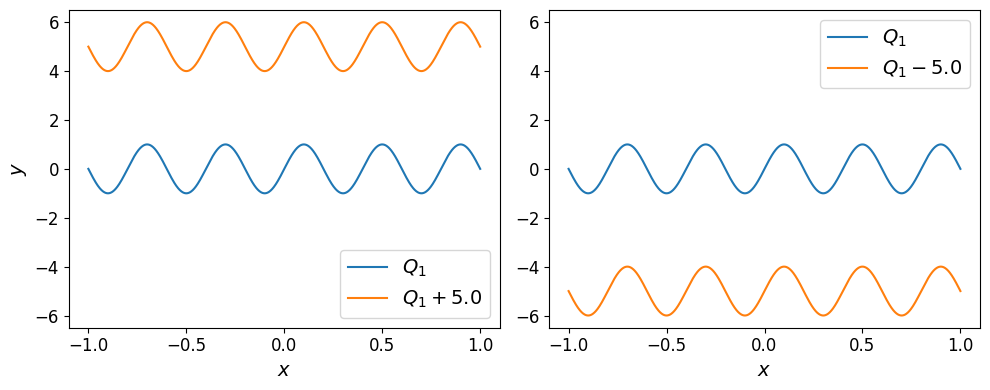
Adding (resp. subtracting) a real scalar number uniformly shifts the polynomial up (resp. down):
Show code cell source
xx_plot = np.linspace(-1, 1, 1000)
fig, axs = plt.subplots(nrows=1, ncols=2, figsize=(10, 4))
axs[0].plot(xx_plot, poly_1(xx_plot), label="$Q_1$")
axs[0].plot(xx_plot, poly_scalar_add(xx_plot), label="$Q_1 + 5.0$")
axs[0].set_xlabel("$x$", fontsize=14)
axs[0].set_ylabel("$y$", fontsize=14)
axs[0].tick_params(axis='both', which='major', labelsize=12)
axs[0].legend(fontsize=14, loc="lower right")
axs[0].set_ylim([-6.5, 6.5])
axs[1].plot(xx_plot, poly_1(xx_plot), label="$Q_1$")
axs[1].plot(xx_plot, poly_scalar_sub(xx_plot), label="$Q_1 - 5.0$")
axs[1].set_xlabel("$x$", fontsize=14);
axs[1].tick_params(axis='both', which='major', labelsize=12)
axs[1].legend(fontsize=14, loc="upper right")
axs[1].set_ylim([-6.5, 6.5])
fig.tight_layout();
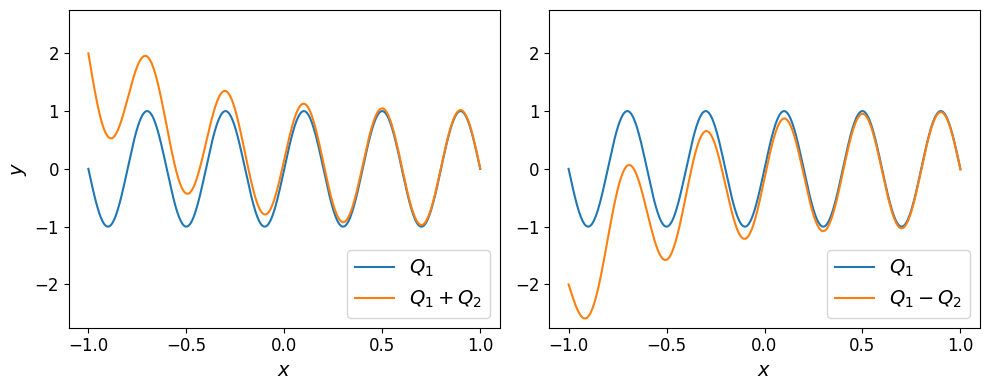
Polynomials may also be added or subtracted from each other; the result is once again another polynomial.
For instance, \(Q_{\mathrm{sum}} = Q_1 + Q_2\):
poly_sum = poly_1 + poly_2
poly_sum
<minterpy.polynomials.newton_polynomial.NewtonPolynomial at 0x7febe6845150>
or \(Q_{\mathrm{diff}} = Q_1 - Q_2\):
poly_diff = poly_1 - poly_2
poly_diff
<minterpy.polynomials.newton_polynomial.NewtonPolynomial at 0x7febe4a7b880>
The plots of the two polynomials are shown below.
Show code cell source
xx_plot = np.linspace(-1, 1, 1000)
fig, axs = plt.subplots(nrows=1, ncols=2, figsize=(10, 4))
axs[0].plot(xx_plot, poly_1(xx_plot), label="$Q_1$")
axs[0].plot(xx_plot, poly_sum(xx_plot), label="$Q_1 + Q_2$")
axs[0].set_xlabel("$x$", fontsize=14)
axs[0].set_ylabel("$y$", fontsize=14)
axs[0].tick_params(axis='both', which='major', labelsize=12)
axs[0].legend(fontsize=14, loc="lower right")
axs[0].set_ylim([-2.75, 2.75])
axs[1].plot(xx_plot, poly_1(xx_plot), label="$Q_1$")
axs[1].plot(xx_plot, poly_diff(xx_plot), label="$Q_1 - Q_2$")
axs[1].set_xlabel("$x$", fontsize=14);
axs[1].tick_params(axis='both', which='major', labelsize=12)
axs[1].legend(fontsize=14, loc="lower right")
axs[1].set_ylim([-2.75, 2.75])
fig.tight_layout();
Multiplication#
Minterpy polynomials may also be multiplied by a real scalar number; the operation returns another polynomial.
Consider \(5 \times Q_2\):
poly_scalar_mul = 5.0 * poly_2
poly_scalar_mul
<minterpy.polynomials.newton_polynomial.NewtonPolynomial at 0x7febe09b6860>
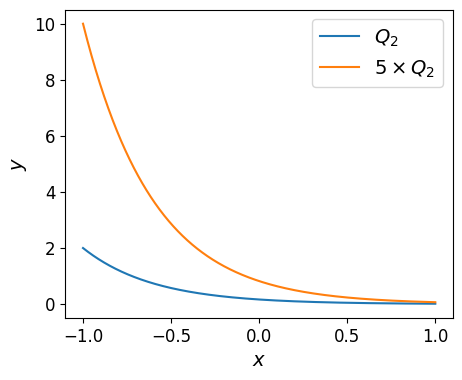
Scalar multiplication uniformly and vertically stretches the polynomial across its domain as shown in the plot below.
Show code cell source
fig, ax = plt.subplots(nrows=1, ncols=1, figsize=(5, 4))
ax.plot(xx_plot, poly_2(xx_plot), label="$Q_2$")
ax.plot(xx_plot, poly_scalar_mul(xx_plot), label="$5 \\times Q_2$")
ax.set_xlabel("$x$", fontsize=14)
ax.set_ylabel("$y$", fontsize=14)
ax.tick_params(axis='both', which='major', labelsize=12)
ax.legend(fontsize=14);
Furthermore, a multiplication between Minterpy polynomials is also a valid operation that returns a polynomial.
For instance, \(Q_{\mathrm{prod}} = Q_1 \times Q_2\):
poly_prod = poly_1 * poly_2
poly_prod
<minterpy.polynomials.newton_polynomial.NewtonPolynomial at 0x7febe0830cd0>
The plot of the product polynomial is shown below:
Show code cell source
xx_plot = np.linspace(-1, 1, 1000)
fig, axs = plt.subplots(nrows=1, ncols=3, figsize=(12, 4))
axs[0].plot(xx_plot, poly_1(xx_plot), label="$Q_1$")
axs[0].set_xlabel("$x$", fontsize=14)
axs[0].set_ylabel("$y$", fontsize=14)
axs[0].tick_params(axis='both', which='major', labelsize=12)
axs[0].legend(fontsize=14, loc="upper right")
axs[0].set_ylim([-2.0, 2.25])
axs[1].plot(xx_plot, poly_2(xx_plot), label="$Q_2$")
axs[1].set_xlabel("$x$", fontsize=14);
axs[1].tick_params(axis='both', which='major', labelsize=12)
axs[1].legend(fontsize=14, loc="upper right")
axs[1].set_ylim([-2.0, 2.25])
axs[2].plot(xx_plot, poly_prod(xx_plot), label="$Q_1 \\times Q_2$")
axs[2].set_xlabel("$x$", fontsize=14)
axs[2].tick_params(axis='both', which='major', labelsize=12)
axs[2].legend(fontsize=14);
axs[2].legend(fontsize=14, loc="upper right")
axs[2].set_ylim([-2.0, 2.25])
fig.tight_layout();
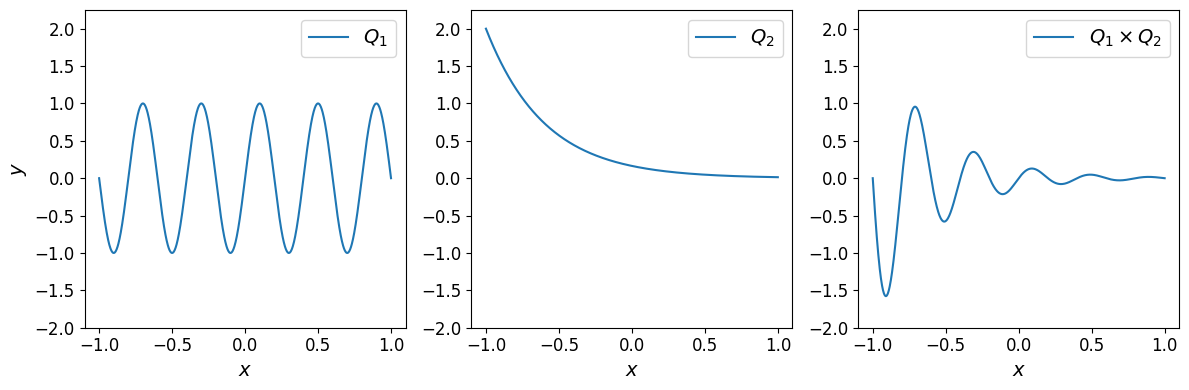
As expected the product polynomial is an exponentially decaying sine function.
Division#
Minterpy polynomials may be divided by a real scalar number; this operation returns another polynomial.
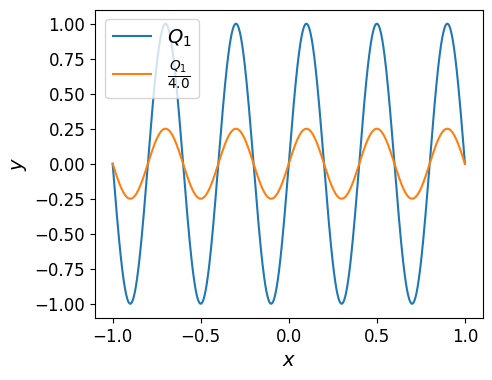
For instance, \(Q_1 / 4.0\):
poly_scalar_div = poly_1 / 4.0
poly_scalar_div
<minterpy.polynomials.newton_polynomial.NewtonPolynomial at 0x7febe0994e20>
Division by a real scalar number uniformly and vertically contracts the polynomial across its domain as shown in the plot below.
Show code cell source
fig, ax = plt.subplots(nrows=1, ncols=1, figsize=(5, 4))
ax.plot(xx_plot, poly_1(xx_plot), label="$Q_1$")
ax.plot(xx_plot, poly_scalar_div(xx_plot), label="$\\frac{Q_1}{4.0}$")
ax.set_xlabel("$x$", fontsize=14)
ax.set_ylabel("$y$", fontsize=14)
ax.tick_params(axis='both', which='major', labelsize=12)
ax.legend(fontsize=14);
Minterpy, however, does not support polynomial-polynomial division (rational function). Minterpy cannot evaluate the resulting function of the expression:
and return the resulting rational function.
Note
That being said, you can still evaluate the evaluation of the expression above at a given set of query points (as long as \(Q_2(x) \neq 0\)).
Exponentiation#
Finally, Minterpy polynomials may also be exponentiated by a non-negative integer. As all the other arithmetic operations above, polynomial exponentiation returns another polynomial.
For instance, \(Q_1^2\):
poly_exp = poly_1**2
poly_exp
<minterpy.polynomials.newton_polynomial.NewtonPolynomial at 0x7febe09f4490>
Show code cell source
fig, ax = plt.subplots(nrows=1, ncols=1, figsize=(5, 4))
ax.plot(xx_plot, poly_1(xx_plot), label="$Q_1$")
ax.plot(xx_plot, poly_exp(xx_plot), label="$Q_1^2$")
ax.set_xlabel("$x$", fontsize=14)
ax.set_ylabel("$y$", fontsize=14)
ax.tick_params(axis='both', which='major', labelsize=12)
ax.legend(fontsize=14);

Raising a polynomial to a non-negative integer power is equivalent to performing multiple-self multiplications of the polynomial.
For instance, \(Q_2^2 = Q_2 \times Q_2\):
poly_2**2 == poly_2 * poly_2
True
or \(Q_2^3 = Q_2 \times Q_2 \times Q_2\):
poly_2**3 == poly_2 * poly_2 * poly_2
True
Finally, raising a polynomial to the power of \(0\) results in a constant polynomial with a value of \(1.0\).
poly_1_exp_0 = poly_1**0
poly_2_exp_0 = poly_2**0
Show code cell source
xx_plot = np.linspace(-1, 1, 1000)
fig, axs = plt.subplots(nrows=1, ncols=2, figsize=(10, 4))
axs[0].plot(xx_plot, poly_1(xx_plot), label="$Q_1$")
axs[0].plot(xx_plot, poly_1_exp_0(xx_plot), label="$Q_1^0$")
axs[0].set_xlabel("$x$", fontsize=14)
axs[0].set_ylabel("$y$", fontsize=14)
axs[0].tick_params(axis='both', which='major', labelsize=12)
axs[0].legend(fontsize=14, loc="lower right")
axs[0].set_ylim([-1.5, 2.25])
axs[1].plot(xx_plot, poly_2(xx_plot), label="$Q_2$")
axs[1].plot(xx_plot, poly_2_exp_0(xx_plot), label="$Q_2^0$")
axs[1].set_xlabel("$x$", fontsize=14);
axs[1].tick_params(axis='both', which='major', labelsize=12)
axs[1].legend(fontsize=14, loc="lower right")
axs[1].set_ylim([-1.5, 2.25])
fig.tight_layout();

Warning
Note that Minterpy polynomials do not support exponentiation by another polynomial, a negative number, or a non-integer value. If you attempt to perform such an operation, an exception will be raised.
Summary#
In this in-depth tutorial, you’ve learned about the basic arithmetic operations involving Minterpy polynomials. Minterpy polynomials are closed under the following arithmetic operations, meaning that the result of the performing these operations is always another Minterpy polynomial:
Polynomial-scalar addition and subtraction
Polynomial-polynomial addition and subtraction
Polynomial-scalar multiplication
Polynomial-polynomial multiplication
Polynomial-scalar division
Polynomial exponentiation by a non-negative integer
Throughout the tutorial, one-dimensional polynomials were used for illustration, but the principles apply similarly to Minterpy polynomials of higher dimensions.
Please note that Minterpy currently does not support:
Polynomial-polynomial division (i.e., forming rational functions)
Polynomial exponentiation by another polynomial or by a real scalar (including negative integers and non-integer numbers)
In the next tutorial, you will explore additional features of Minterpy, including basic calculus operations such as differentiation and integration.
