Create a Grid with a Generating Function#

import numpy as np
import minterpy as mp
import matplotlib.pyplot as plt

Minterpy interpolating polynomials (i.e., in the Lagrange or Newton basis) lives on a grid that holds the so-called unisolvent nodes. An interpolating multi-dimensional polynomial of a given multi-index set of exponents is uniquely determined on the corresponding unisolvent nodes.

An instance of Grid can be constructed via different constructors:

Grid.from_function(): create an instance with a generating function (this page)
Grid.from_points(): create an instance with an array of generating points (see the example)
Grid.from_degree(): create an instance with a complete multi-index set (see the example)
Grid.from_value_set(): create an instance based on an array of generating values (see the example)
Grid: the default constructor (see the example)

This guide provides an example on how to construct a Grid instance based on a given generating function using the from_function() method.

About a generating function#

A generating function is a function that creates an array of generating points (nodes) for a given one-dimensional polynomial degree and spatial dimension. It then returns an array of shape (n + 1, m) where n and m are the one-dimensional polynomial degree and spatial dimension, respectively.

A valid generating function in Minterpy must have a signature similar to the one below:

def my_gen_fun(poly_degree: int, spatial_dimension: int) -> np.ndarray:
    ...

It must return an array with the aforementioned shape and each column of the array must have unique values.

Take for instance, the default generating function in Minterpy, i.e., the Leja-ordered Chebyshev-Lobatto generating function. The function returns the following generating points in two dimensions with maximum polynomial degree of \(3\) in every dimension:

mp.gen_points.gen_points_chebyshev(poly_degree=3, spatial_dimension=2)

array([[ 1. , -1. ],
       [-1. ,  1. ],
       [ 0.5, -0.5],
       [-0.5,  0.5]])

Notice that the array has \(4\) rows (i.e., \(n + 1\), \(n = 3\) as one-dimensional polynomials of degree \(3\) require \(4\) points) and \(2\) columns (i.e., \(m = 2\)), and that each column has unique values.

About the `from_function()` factory method#

The method from_function() of the Grid class returns an instance of Grid based on a given generating function.

The method accepts two mandatory arguments, namely, the multi-index set of exponents that defines the polynomials that grid can support, and the generating function that creates generating points as required by the multi-index set.

Any callable that is a valid generating function (see above) may be passed as the second argument to from_function(). Alternatively, a string as a key to a dictionary of built-in generating functions may be specified.

The from_function() method is a shortcut to create a grid with a given multi-index set and a particular generating function that is, possibly, defined by the users.

Example: Two-dimensional interpolation grid#

Create an equidistant interpolation grid in \([-1, 1]^2\) to support two-dimensional polynomials having a multi-index set \(A = \{ (0, 0), (1, 0), (2, 0), (3, 0), (0, 1), (1, 1), (0, 2), (1, 2), (0, 3), (0, 4) \}\) (defined with respect to \(l_p\)-degree \(2.0\)).

Multi-index set#

Create an instance of MultiIndexSet following the above specification:

exponents = np.array([
    [0, 0],
    [1, 0],
    [2, 0],
    [3, 0],
    [0, 1],
    [1, 1],
    [0, 2],
    [1, 2],
    [0, 3],
    [0, 4],
])

mi = mp.MultiIndexSet(exponents, lp_degree=2.0)

print(mi)

MultiIndexSet(m=2, n=4, p=2.0)
[[0 0]
 [1 0]
 [2 0]
 [3 0]
 [0 1]
 [1 1]
 [0 2]
 [1 2]
 [0 3]
 [0 4]]

Generating function#

The generating function for equidistant points can be defined as follows:

def equidistant_gen_function(
    poly_degree: int,
    spatial_dimension: int,
) -> np.ndarray:
    """Create an array of equidistant generating points."""
    xx = np.linspace(-1, 1, poly_degree + 1)[:, np.newaxis]
    
    return np.tile(xx, spatial_dimension)

Given the function above, the generating points for polynomial degree \(3\) in every dimension and spatial dimension \(3\) are:

print(equidistant_gen_function(3, 3))

[[-1.         -1.         -1.        ]
 [-0.33333333 -0.33333333 -0.33333333]
 [ 0.33333333  0.33333333  0.33333333]
 [ 1.          1.          1.        ]]

Grid instance#

Given the multi-index set and the generating function, an instance of Grid can be constructed via the from_function() method as follows:

grd = mp.Grid.from_function(mi, equidistant_gen_function)

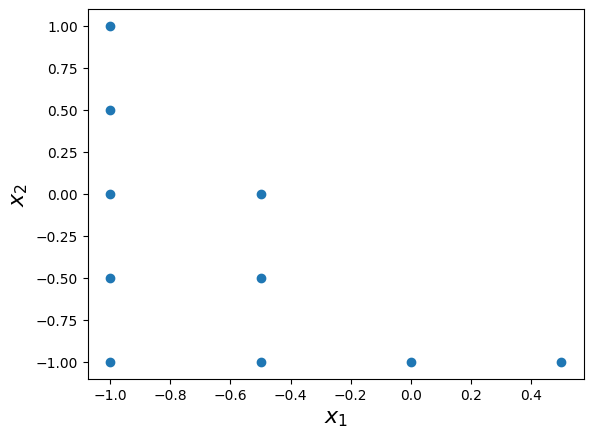
The grid has the following unisolvent nodes:

print(grd.unisolvent_nodes)

[[-1.  -1. ]
 [-0.5 -1. ]
 [ 0.  -1. ]
 [ 0.5 -1. ]
 [-1.  -0.5]
 [-0.5 -0.5]
 [-1.   0. ]
 [-0.5  0. ]
 [-1.   0.5]
 [-1.   1. ]]

Finally, the two-dimensional interpolation grid is plotted below:

plt.scatter(grd.unisolvent_nodes[:, 0], grd.unisolvent_nodes[:, 1])
plt.xlabel("$x_1$", fontsize=16)
plt.ylabel("$x_2$", fontsize=16);

../../_images/8d14e93b1eb7301a4020017653e24e56719df5492363fc0f009060ef428a4706.png