Create a Grid with a Complete Multi-Index Set#

import numpy as np
import minterpy as mp
import matplotlib.pyplot as plt

Minterpy interpolating polynomials (i.e., in the Lagrange or Newton basis) lives on a grid that holds the so-called unisolvent nodes. An interpolating multi-dimensional polynomial of a given multi-index set of exponents is uniquely determined on the corresponding unisolvent nodes.

An instance of Grid can be constructed via different constructors:

This guide provides an example on how to construct a Grid instance with a complete multi-index set using the from_degree() method.

About complete multi-index sets#

A complete multi-index set with respect to spatial dimension \(m\), polynomial degree \(n\), and \(l_p\)-degree \(p\) denoted by \(A_{m, n, p}\) contains all the exponents \(\boldsymbol{\alpha} = (\alpha_1, \ldots, \alpha_m) \in \mathbb{N}^m\) such that the \(l_p\)-norm \(\lVert \boldsymbol{\alpha} \rVert_p \leq n\) holds.

A complete multi-index set is a typical way (but by no means, the only way) to define a multi-index set of exponents in Minterpy.

About from_degree() factory method#

The method from_degree() of the Grid class returns an instance of Grid based on the specification of a complete multi-index set and optionally, the generating function and the generating points.

The method accepts the following arguments:

  • spatial_dimension (\(m\)): the dimension of the multi-index set and subsequently, the grid.

  • poly_degree (\(n\)): the polynomial degree of the set.

  • lp_degree (\(p\)): the \(l_p\)-degree with respect to which the complete multi-index set is defined.

  • generating_function: the generating function to create an array of generating points required by the complete multi-index set. This argument is optional; if not specified, the default Leja-ordered Chebyshev-Lobatto generating function is selected. For detail regarding a valid generating function, see the corresponding example.

  • generating_points: the generating points of the interpolation grid. This argument is optional; if not specified, the points are generated by the generating function as required. For detail regarding valid generating points, see the corresponding example.

The from_degree() method is a shortcut for constructing a grid that corresponds to a complete multi-index set; it avoids the separate construction of a complete MultiIndexSet instance that is then passed to the other constructors of the Grid class.

Example: Two-dimensional interpolation grid#

Create an interpolation grid that can support two-dimensional polynomials defined by a complete multi-index set of polynomial degree \(3\) with respect to \(l_p\)-degree \(\infty\) and with Leja-ordered Chebyshev-Lobatto points as the generating points.

An instance of Grid that satisfies the above condition can be created using from_degree() method as follows:

grd = mp.Grid.from_degree(
    spatial_dimension=2,
    poly_degree=3,
    lp_degree=np.inf,
)

As the Leja-ordered Chebyshev-Lobatto points are the generating function selected by default, no specification is required.

The grid has the following unisolvent nodes:

print(grd.unisolvent_nodes)

[[ 1.  -1. ]
 [-1.  -1. ]
 [ 0.5 -1. ]
 [-0.5 -1. ]
 [ 1.   1. ]
 [-1.   1. ]
 [ 0.5  1. ]
 [-0.5  1. ]
 [ 1.  -0.5]
 [-1.  -0.5]
 [ 0.5 -0.5]
 [-0.5 -0.5]
 [ 1.   0.5]
 [-1.   0.5]
 [ 0.5  0.5]
 [-0.5  0.5]]

The two-dimensional interpolation grid is plotted below:

plt.scatter(grd.unisolvent_nodes[:, 0], grd.unisolvent_nodes[:, 1])
plt.xlabel("$x_1$", fontsize=16)
plt.ylabel("$x_2$", fontsize=16);
../../_images/21f229247fd65ff7988ca0f8d2f4fb431f955688e891806e375554a2a4ab1114.png

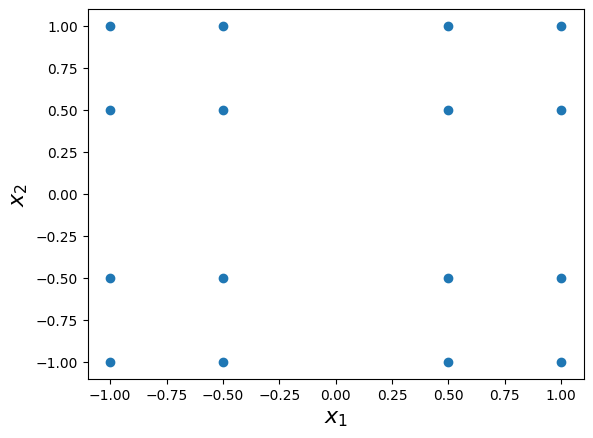
This interpolation grid corresponds to the full tensorial grid of two-dimensional polynomials with polynomial degree of \(3\).