One-Dimensional Polynomial Interpolation#

Welcome to the first in-depth tutorial of Minterpy!

Minterpy is an open source Python package for carrying out numerical tasks with multivariate (multi-dimensional) polynomials. You can do a wide range of arithmetic and calculus operations with Minterpy polynomials.

But how to create such polynomials in the first place?

This tutorial demonstrates how you can create such a polynomial from scratch in the most typical use case: interpolating a function.

Import Minterpy#

After installing installing Minterpy, you can import it as follows:

import minterpy as mp

The shorthand mp is the convention we, the developer team, like to use; it’s short and recognizable (just like np for NumPy and pd for pandas).

You will also need to import NumPy and Matplotlib to follow along with this guide.

import numpy as np
import matplotlib.pyplot as plt

Motivating function#

In Minterpy, polynomials are typically used to approximate functions of interest by interpolating them. This is actually one of the main goals of Minterpy: to approximate a (multidimensional) function using a polynomial.

For now, however, consider the following one-dimensional function:

\[ f(x) = \frac{1}{1 + 25 x^2}, x \in [-1, 1]. \]

Define this function in Python:

fun = lambda x: 1 / (1 + 25 * x**2)

The plot of the function is shown below.

Hide code cell source 
xx = np.linspace(-1, 1, 300)
plt.plot(xx, fun(xx))
plt.xlabel("$x$", fontsize=14)
plt.ylabel("$y$", fontsize=14)
plt.tick_params(axis='both', which='major', labelsize=12)
../_images/af10d8d6fa7534a4309617824472ec4b39bf01434cb3576c4ada4eb069075912.png

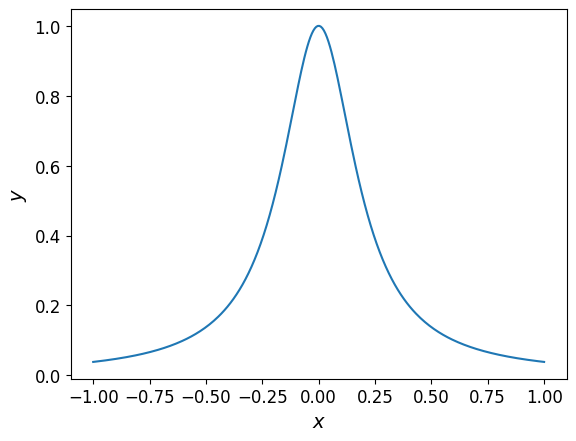
Now that you’ve defined your function, you’re ready to create a polynomial that approximates it.

Create an interpolating polynomial#

To create an interpolating polynomial from scratch in Minterpy, follow these four main steps:

  1. Define the multi-index set: Specify the multi-index set that determines the structure of the polynomial.

  2. Construct an interpolation grid: Create an interpolation grid, which consists of the points at which the function of interest will be evaluated.

  3. Evaluate the function of interest at the grid points: Compute the function values at the grid points (also known as the unisolvent nodes)

  4. Create a polynomial in the Lagrange basis: Construct the interpolating polynomial in the Lagrange basis based on the evaluated points.

To perform additional operations with the interpolating polynomial, such as evaluating it at a set of query points, follow this extra step:

  1. Transform the polynomial to another basis: Change the basis of the interpolating polynomial from the Lagrange basis to another basis, preferably the Newton basis, for convenient evaluation and manipulation.

Let’s go through these steps one at a time.

Define a multi-index set#

In Minterpy, the exponents of a multivariate polynomial are represented using multi-indices within a set known as the multi-index set. This set generalizes the notion of polynomial degree to multiple dimensions. For more details, see the the relevant section of the documentation.

Even though our function is one-dimensional, defining the multi-index set (in this case, of dimension \(1\)) is still the first steps of constructing a Minterpy polynomial.

In Minterpy, multi-index sets are represented by the MultiIndexSet class. You can create a complete multi-index set using the class method from_degree(), which requires the spatial dimension (first argument) and the polynomial degree (second argument).

To construct a one-dimensional multi-index set of polynomial degree, say, \(10\), type:

mi = mp.MultiIndexSet.from_degree(1, 10)

This produces the following instance:

mi

MultiIndexSet(
  array([[ 0],
         [ 1],
         [ 2],
         [ 3],
         [ 4],
         [ 5],
         [ 6],
         [ 7],
         [ 8],
         [ 9],
         [10]]),
  lp_degree=2.0
)

Construct an interpolation grid#

An interpolation grid is where an interpolating polynomial lives on. The bases of interpolating polynomials, such as the Lagrange or the Newton basis, are built with respect to these grids.

In Minterpy, interpolation grids are represented by the Grid class. The default constructor allows you to create an interpolation grid for a specified multi-index set (the first argument).

To create an interpolation grid for the previously defined multi-index set, use the following command:

grd = mp.Grid(mi)

An instance of Grid is always defined with respect to a multi-index set. In simple terms, the multi-index set of an interpolation grid determines the structure of multivariate polynomials that the grid can support.

A key property of a Grid instance is unisolvent_nodes (i.e., interpolating nodes or grid points). These nodes are crucial because they uniquely determine the interpolating polynomial given the multi-index set. By default, Minterpy generates unisolvent nodes based on the Leja-ordered Chebyshev-Lobatto points. For the chosen polynomial degree, these nodes are:

grd.unisolvent_nodes

array([[ 1.00000000e+00],
       [-1.00000000e+00],
       [-6.12323400e-17],
       [ 5.87785252e-01],
       [-5.87785252e-01],
       [ 8.09016994e-01],
       [-8.09016994e-01],
       [ 3.09016994e-01],
       [-3.09016994e-01],
       [ 9.51056516e-01],
       [-9.51056516e-01]])

which distributed like the following:

Hide code cell source 
ax = plt.axes(frameon=False)
ax.get_xaxis().tick_bottom()
ax.axes.get_yaxis().set_visible(False)
ax.scatter(grd.unisolvent_nodes.reshape(-1), np.zeros(len(grd.multi_index)), marker="x", color="black")
ax.set_ylim([-0.01, 0.01])
ax.hlines(0, -1, 1, linewidth=0.5, linestyle="--", color="black")
ax.set_title("Interpolation grid");
plt.show()
../_images/f15752a36c9f56ae691f3946558a5c8e5328372967084481d3f444d3ba9efac5.png

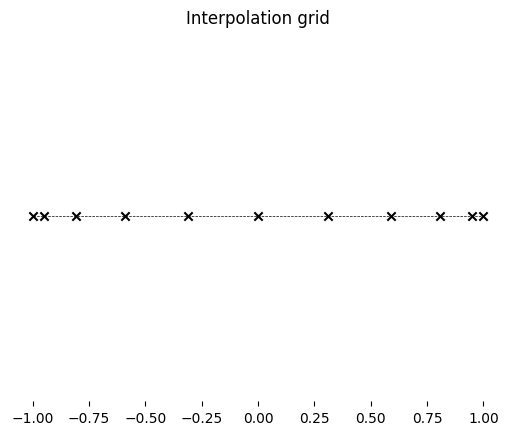
Notice that there are more points in the boundaries of the domain.

Evaluate the function at the unisolvent nodes#

An interpolating polynomial \(Q\) with a domain of \([-1, 1]\) of a function \(f\) is a polynomial that satisfies the following condition:

\[ Q(p_{\alpha}) = f(p_{\alpha}), \forall p_{\alpha} \in P_A, \]

where \(P_A = \{ p_{\alpha} \}\) is the set of unisolvent nodes.

The function values at the unisolvent nodes are therefore crucial to construct an interpolating polynomial.

In Minterpy, calling an instance of Grid with a given function evaluates the function at the unisolvent nodes:

coeffs = grd(fun)
coeffs

array([[0.03846154],
       [0.03846154],
       [1.        ],
       [0.10376364],
       [0.10376364],
       [0.05759469],
       [0.05759469],
       [0.29522147],
       [0.29522147],
       [0.04235007],
       [0.04235007]])

Create a Lagrange polynomial#

The function values at the unisolvent nodes are equal to the coefficients of a polynomial in the Lagrange basis \(c_{\mathrm{lag}, \alpha}\):

\[ Q(x) = \sum_{\alpha \in A} c_{\mathrm{lag}, \alpha} \Psi_{\mathrm{lag}, \alpha}(x), \]

where \(A\) is the multi-index set and \(\Psi_{\alpha}\)’s are Lagrange basis polynomials, each of which satisfies:

\[ \Psi_{\mathrm{lag}, \alpha}(p_{\beta}) = \delta_{\alpha, \beta}, p_\beta \in P_A, \]

where \(\delta{\cdot, \cdot}\) denotes the Kronecker delta.

Polynomials in the Lagrange basis are represented by the LagrangePolynomial class in Minterpy. You can create an instance of LagrangePolynomial class with various constructors. Relevant to the present tutorial, from_grid() constructor accepts an instance of Grid and the corresponding Lagrange coefficients (i.e., function values at the unisolvent nodes) to create an instance of LagrangePolynomial.

lag_poly = mp.LagrangePolynomial.from_grid(grd, coeffs)

Congratulations! You’ve just made your first polynomial in Minterpy from scratch.

Transform to the Newton basis#

Unfortunately, polynomials in the Lagrange basis have limited functionality; for instance, you can’t directly evaluate them at a set of query points.

In Minterpy, the Lagrange basis primarily serves as a convenient starting point for constructing an interpolating polynomial. The coefficients in this basis are straightforwardly defined as the function values at the unisolvent nodes (grid points).

To perform more advanced operations with the polynomial in Minterpy, you need to transform it into the Newton basis. In the Newton basis, the polynomial takes the form:

\[ Q(x) = \sum_{\alpha \in A} c_{\mathrm{nwt}, \alpha} \, \Psi_{\mathrm{nwt}, \alpha}(x), \]

where \(c_{\mathrm{nwt}, \alpha}\)’s are the coefficients of the polynomial in the Newton basis and \(\Psi_{\mathrm{nwt}, \alpha}\) is the the Newton basis polynomial associated with multi-index element \(\alpha\):

\[ \Psi_{\mathrm{nwt}, \alpha}(x) = \prod_{i = 0}^{\alpha - 1} (x - p_i), \]

where \(p_i\)’s are the interpolation points (unisolvent nodes).

To transform a polynomial in the Lagrange basis to a polynomial in the Newton basis, use the LagrangeToNewton class:

nwt_poly = mp.LagrangeToNewton(lag_poly)()

/home/runner/work/minterpy/minterpy/src/minterpy/schemes/barycentric/transformation_fcts.py:109: NumbaPerformanceWarning: '@' is faster on contiguous arrays, called on (Array(float64, 2, 'A', False, aligned=True), Array(float64, 1, 'C', False, aligned=True))
  coeff_slice_transformed = matrix_piece @ slice_in

In the above statement, the first part of the call, mp.LagrangeToNewton(lag_poly), creates a transformation instance that converts the given polynomial from the Lagrange basis to the Newton basis.

The second call, which is made without any arguments, performs the transformation and returns the actual Newton polynomial instance.

Note

Minterpy offers other polynomial bases as well, but for most practical purposes, we recommend to use the Newton basis.

Evaluate the polynomial at a set of query points#

Once a polynomial in the Newton basis is obtained, you can evaluate it at a set of query points; this one of the most routine tasks involving polynomial approximation.

First, create a set of equally spaced test points in \([-1, 1]\):

xx_test = np.linspace(-1, 1, 1000)

Then evaluate the original function at these points:

yy_test = fun(xx_test)

Calling an instance of NewtonPolynomial at these query points evaluate the polynomial at the query points:

yy_poly = nwt_poly(xx_test)
yy_poly[:5]

array([0.03846154, 0.04058527, 0.04244967, 0.0440694 , 0.0454586 ])

As expected, evaluating the polynomial on \(1'000\) query points returns an array \(1'000\) points:

yy_poly.shape

(1000,)

Note

For evaluation, an instance of polynomial expects as its input an array; as the polynomial is one dimensional, the array should either be one-dimensional or two-dimensional with a single column (the column of a two-dimensional array indicates the values along each spatial dimension).

Let’s compare the results of the interpolating polynomial with the original function.

Hide code cell source 
plt.plot(xx_test, yy_test, label="true function ($f$)")
plt.plot(xx_test, yy_poly, label="interpolant ($Q$)")
plt.xlabel("$x$", fontsize=14)
plt.ylabel("$y$", fontsize=14)
plt.scatter(grd.unisolvent_nodes, lag_poly.coeffs, label="unisolvent nodes")
plt.tick_params(axis='both', which='major', labelsize=12)
plt.legend();
../_images/d4c203920d437b628c3052a7cce45562a127058edd28b32040d1ce96dea47e0b.png

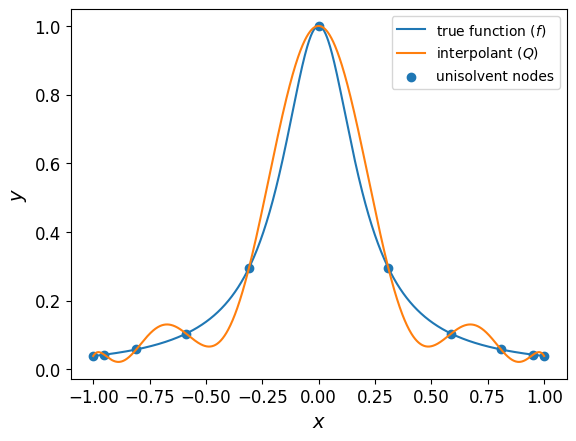
The plot also shows the location of the unisolvent nodes and their corresponding function values; the interpolant is indeed interpolatory.

Assess the accuracy of interpolating polynomial#

As shown in the plot above, the chosen polynomial degree is not accurate enough to approximate the true function.

The infinity norm provides a measure of the greatest error of the interpolant over the whole domain. The norm is defined as:

\[ \lVert f - Q \rVert_\infty = \sup_{-1 \leq x \leq 1} \lvert f(x) - Q(x) \rvert \]

The infinity norm of \(Q\) can be approximated using the \(1'000\) testing points created above:

np.max(np.abs(yy_test - yy_poly))

np.float64(0.1321948529511282)

which is hardly a numerical convergence.

The interpolate() function#

As an alternative to constructing an interpolating polynomial from scratch using the steps outlined above, you can use the interpolate() function. The function allows you to specify:

  • the function to interpolate

  • the number of dimensions

  • the degree of polynomial interpolant

All in a single function call. The function returns a callable object that you can use to evaluate the (underlying) interpolating polynomial at a set of query points.

To create an interpolant using the interpolate() function with the same structure as before, use the following command:

q = mp.interpolate(fun, spatial_dimension=1, poly_degree=10)

The resulting interpolant can be evaluated at a set of query points:

q(xx_test)[:5]

array([0.03846154, 0.04058527, 0.04244967, 0.0440694 , 0.0454586 ])

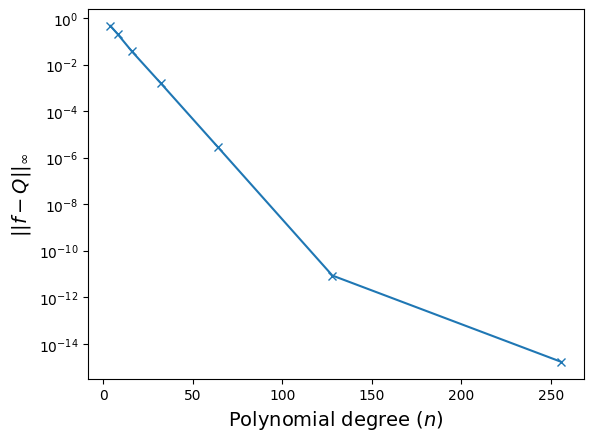
With this shortcut to create an interpolant where evaluation is all that is needed, let’s investigate the convergence of interpolating polynomials with increasing polynomial degrees.,

poly_degrees = [4, 8, 16, 32, 64, 128, 256]
yy_poly = np.empty((len(xx_test), len(poly_degrees)))
for i, n in enumerate(poly_degrees):
    fx_interp = mp.interpolate(fun, spatial_dimension=1, poly_degree=n)
    yy_poly[:, i] = fx_interp(xx_test)

The interpolants of increasing degrees looks like:

Hide code cell source 
plt.plot(xx_test, yy_test);
for i, n in enumerate(poly_degrees):
    plt.plot(xx_test, yy_poly[:, i], label="degree = {}".format(n))
plt.xlabel("$x$", fontsize=14)
plt.ylabel("$y$", fontsize=14)
plt.legend();
../_images/1ce777da8b71b1be223d0e1f18a22e16f24df6945f9077acd44be151bcb1b79d.png

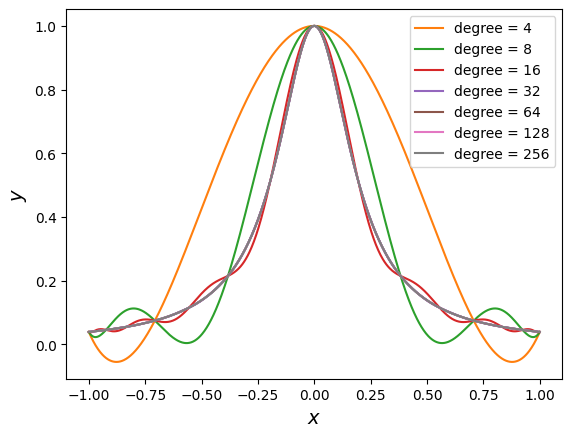
The convergence of the error is shown below:

errors = np.max(np.abs(yy_test[:, np.newaxis] - yy_poly), axis=0)
Hide code cell source 
plt.plot(poly_degrees, errors, '-x');
plt.ylabel(r"$|| f - Q ||_\infty$", fontsize=14)
plt.xlabel("Polynomial degree ($n$)", fontsize=14)
plt.yscale("log");
../_images/02f90aeeb5591f90f01124a87dcad107dce3fb3ff941d069b88f43c94472e278.png

The absolute error of the degree 64 polynomials in the domain is shown below:

Hide code cell source 
plt.plot(xx_test, np.abs(yy_test - yy_poly[:, -1]))
plt.ylim(1e-18,1)
plt.ylabel(r"$| f - Q |$", fontsize=14)
plt.xlabel("$x$", fontsize=14)
plt.yscale("log");
../_images/322d5f7fa25edc00c25a3ccfc25308e076b245a9a1a7f4d15f27ce08ee77a583.png

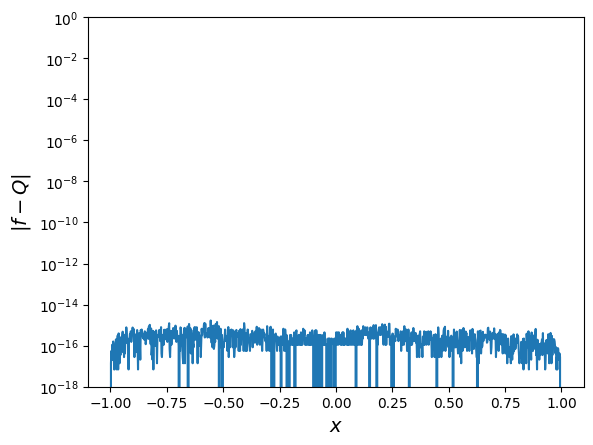
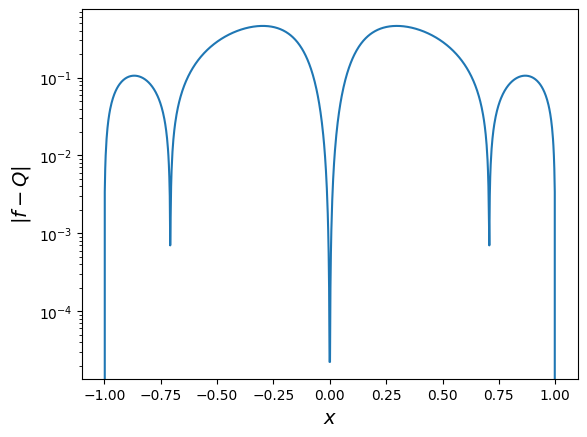
The seemingly random behavior of the (very small) absolute error indicates that machine precision has been reached. Compare it with the absolute error of degree 4 polynomials:

plt.plot(xx_test, np.abs(yy_test - yy_poly[:, 0]))
plt.ylabel(r"$| f - Q |$", fontsize=14)
plt.xlabel("$x$", fontsize=14)
plt.yscale("log");
../_images/ad25c9856bfe9db9da52cdb517a76c9a8fe8997084f00ab0bdbe421148890dbb.png

From Interpolant to polynomial#

The callable produced by interpolate() is an instance of Interpolant; it is not a Minterpy polynomial!

There are, however, convenient methods to represent the interpolant in one of the Minterpy polynomials. These methods are summarized in the table below.

Method

Return the interpolant as a polynomial in the…

to_newton()

NewtonPolynomial

to_lagrange()

LagrangePolynomial

to_canonical()

CanonicalPolynomial

to_chebyshev()

ChebyshevPolynomial

These bases will be the topic of Polynomial Bases and Transformations in-depth tutorial.

For now to obtain the interpolating polynomial in the Newton basis, call:

fx_interp.to_newton()

<minterpy.polynomials.newton_polynomial.NewtonPolynomial at 0x7fbf615f18a0>

Summary#

Congratulations on completing the first in-depth tutorial of Minterpy!

In this tutorial, you’ve learned how to create an interpolating polynomial from scratch in Minterpy to approximate a given function and evaluate it at a set of query points. Specifically, you covered:

  1. Defining a multi-index set: Establishing the structure of the polynomial.

  2. Constructing an interpolation grid: Creating the grid points (unisolvent nodes) for interpolation.

  3. Evaluating the given function on the grid points: Computing function values at the nodes.

  4. Constructing a polynomial in the Lagrange basis: Creating an interpolating polynomial in the Lagrange basis with the function values as the coefficients.

  5. Transform the polynomial into the Newton basis: Changing the basis from the Lagrange basis to the Newton basis for more flexibility.

You’ve also explored the interpolate() function, which simplifies the process of creating an interpolant.

Finally, you’ve learned how to assess the accuracy of an interpolating polynomial as an approximation of the given function and how to investigate its empirical convergence by adjusting the polynomial degree.

Minterpy, as its name implies, supports the construction of multivariate polynomials as well. The process for constructing these polynomials follows similar steps to those described here.

In the next tutorial, you’ll learn how to create multivariate polynomials to interpolate multidimensional functions using Minterpy.