Quick Start Guide to Function Approximations with Minterpy#

Welcome to the Quickstart Guide to Minterpy!

If you’re reading this, chances are you want to create an interpolant that approximates a function, possibly in multiple dimensions. This guide provides a quick walkthrough on how to achieve this using Minterpy.

How to import Minterpy#

After installing installing Minterpy, you can import it as follows:

import minterpy as mp

The shorthand mp is the convention we, the developer team, like to use. You’re free to choose any shorthand you prefer, but we find mp to be both short and recognizable (similar to np for NumPy and pd for pandas).

While you’re at it, you will also need to import Numpy and Matplotlib to follow along with this guide.

import numpy as np
import matplotlib.pyplot as plt

One-dimensional function#

Let’s start with interpolating the following one-dimensional function:

\[ f(x) = x \, \sin{(12 x)}, x \in [-1, 1]. \]

Note

Currently, Minterpy only supports interpolating functions defined in \([-1, 1]^m\) where \(m\) is the spatial dimension. If the domain of your function differs, then you’re responsible to carry out the domain transformation.

You can define the function above using lambda function:

fun_1d = lambda xx: xx * np.sin(12 * xx)

When plotted, the function looks like this:

../_images/97da9095c8fc9c605ddaf684f9aab63a5091d1e65c3e2d316ebee027766492f5.png

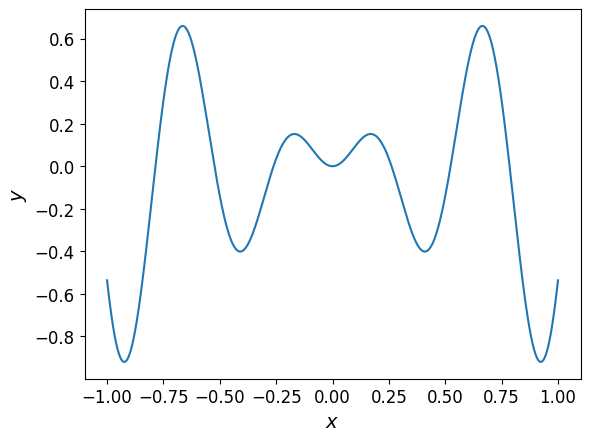
One-dimensional interpolant#

To create an interpolant in Minterpy, use the interpolate() function which accepts the following arguments in order:

The function to interpolate (a callable that takes an array of input values and returns an array of output values of the same length)
The spatial dimension of the function
The degree of the polynomial interpolant

The lambda function you’ve defined above already satisfies the first requirement: as a callable, it takes an array of input values and returns an array of output values.

The spatial dimension of the function, which represents the number of input variables it accepts, is \(1\). Since Minterpy cannot automatically infer the dimensionality of your function, you must specify this value explicitly.

Finally, you need to specify the degree of the polynomial interpolant. Because Minterpy interpolants are based on polynomials, it is necessary to choose the polynomial degree in advance. As a best practice, it is recommended to verify the accuracy of the interpolant after creation to ensure it meets your requirements.

For instance, let’s say you choose a polynomial degree of \(8\):

interp_1d = mp.interpolate(fun_1d, spatial_dimension=1, poly_degree=8)
interp_1d

Interpolant()

Congratulations on creating your first interpolant in Minterpy!

Having obtained an interpolant, you can evaluate it at a set of query points:

xx_test_1d = np.linspace(-1, 1, 1000)  # 1000 query points
interp_1d(xx_test_1d)[:10]  # Show the first 10

array([-0.53657292, -0.57490919, -0.61118339, -0.64544674, -0.67774961,
       -0.70814161, -0.73667155, -0.76338745, -0.78833657, -0.81156539])

The plot of the interpolant is shown below along with the original function:

../_images/d183b9c33ae44d223ddddf642626c84210aff9a2cbbb8347db918b4b2e91bed4.png

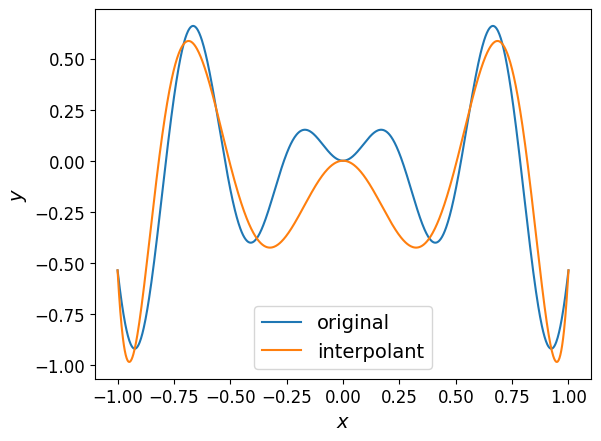
However, the interpolant doesn’t quite match the function as closely as we’d like.

Assessing 1D interpolant accuracy#

Looking at the plot above, you might conclude that the interpolant is not accurate enough as an approximation of the original function. However, relying on a plot to draw such conclusions is not always possible, especially when dealing with functions in higher dimensions.

The infinity norm provides a quantitative measure of the greatest error of the interpolant over the entire domain of the function. It is defined as:

\[ \lVert f - Q \rVert_\infty = \sup_{-1 \leq x \leq 1} \lvert f(x) - Q(x) \rvert \]

where \(Q\) is the interpolant.

You can estimate the infinity norm based on the \(1'000\) query points as follows:

np.max(np.abs(fun_1d(xx_test_1d) - interp_1d(xx_test_1d)))

np.float64(0.4210121066955669)

Whether the given norm is low enough depends on what you’re using the interpolant for. But for now, let’s agree that the number above isn’t exactly a numerical convergence.

To have a more accurate interpolant, increase the polynomial degree, say to \(32\):

interp_1d_32 = mp.interpolate(fun_1d, spatial_dimension=1, poly_degree=32)

The plot of the interpolant is shown below.

../_images/7becc1324fc4e0d161e96ee252f06b5a0cbc28ee5702fbb615170c2dcd923828.png

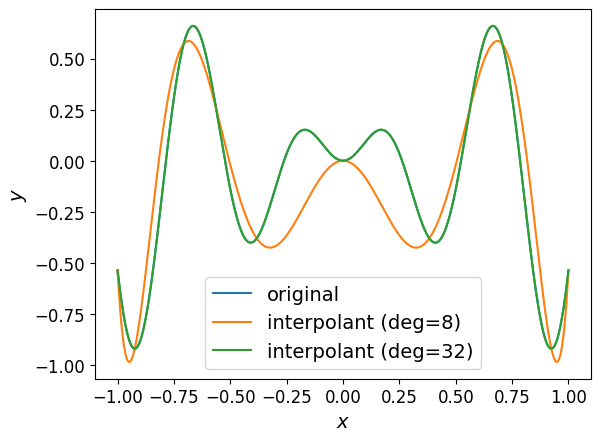
Looking at the graph, it’s hard to see any difference between the interpolant of degree \(32\) and the original function.

Looking at the infinity norm:

np.float64(3.6330938257833623e-12)

which is now closer to numerical convergence.

Two-dimensional function#

Consider now a two-dimensional function:

\[ f(x_1, x_2) = \sin{\pi (1.5 x_1 + 2.5 x_2)}, x_1, x_2 \in [-1, 1]. \]

Below is the code to define the function above in Python as a regular function:

def fun_2d(xx):
    return np.sin(np.pi * (1.5 * xx[:, 0] + 2.5 * xx[:, 1]))

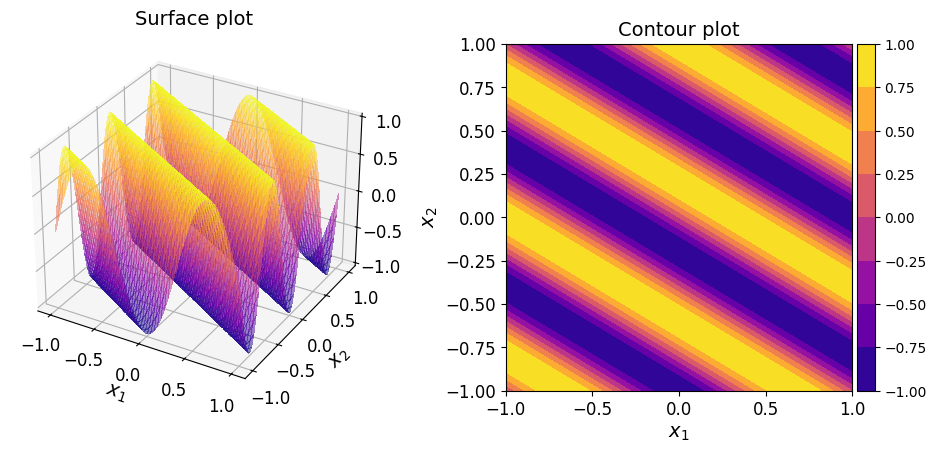
The surface and contour plots of the function are given below.

../_images/07111effcefedd46974bbacee9a389072054a885e40eed590a43ce776da27c0b.png

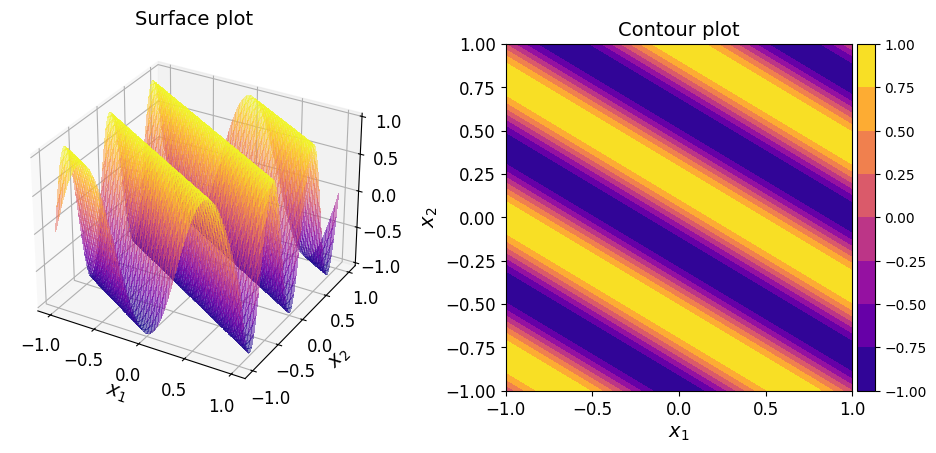
Two-dimension interpolant#

The function interpolate() can also handle two-dimensional functions. Here are a few things to note:

Your function should take a two-dimensional (2D) array as input, where each row represents a point in space and each column corresponds to a spatial dimension. For functions defined in 2D space, this means the input array must have exactly two columns. The function should return an array with the same number of rows as the input.
As mentioned earlier, make sure to specify that your function has a spatial dimension of \(2\) when calling interpolate().

One more thing to note: when you’re working with functions of more than one spatial dimension, you can also specify the \(l_p\)-degree argument. This controls the underlying multi-index set of exponents used in the interpolation. Different \(l_p\)-degree values can affect how well the interpolant approximates the original function. Checkout the relevant section for details. If you don’t specify an \(l_p\)-degree, it defaults to \(2.0\).

To create a two-dimensional interpolant with a polynomial degree of \(32\), use the following command:

interp_2d = mp.interpolate(fun_2d, spatial_dimension=2, poly_degree=32)

The surface and contour plots of the interpolant are shown below.

../_images/05b3ca58d9e1c852c9ffb4f74acfbb66e9644b316d266331b9d6bcfdd50121a0.png

Assessing 2D interpolant accuracy#

Just by looking at the plot, it’s though to say for sure if the interpolant is accurate enough. But it does seem to capture the overall shape of the function pretty well.

As explained previously, you can use the infinity norm to quantify the accuracy of the interpolant. To estimate it using, say, \(100'000\) random points in \([-1, 1]^2\):

rng = np.random.default_rng(194)
xx_test_2d = -1 + 2 * rng.random((100000, 2))
np.max(np.abs(fun_2d(xx_test_2d) - interp_2d(xx_test_2d)))

np.float64(1.8096635301390052e-14)

The choice of polynomial degree seems to be already results in a highly accurate interpolant.

Four-dimensional function#

So far, you’ve seen how to interpolate 1D and 2D functions. But what about functions with even more dimensions?

Consider now the \(m\)-dimensional Runge function:

\[ f(\boldsymbol{x}) = \frac{1}{1 + 1.0 \lVert \boldsymbol{x} \rVert_2^2}, \boldsymbol{x} \in [-1, 1]^m. \]

The function can be computed for any arbitrary dimension, but for this tutorial, the dimension is set to \(4\) which already makes it hard to visualize.

Note

The classic Runge function has a factor of \(25\) instead of \(1.0\) which makes the above function “easier” to interpolate.

To define the function above as a lambda function:

fun_md = lambda xx: 1 / (1 + 1.0 * np.sum(xx**2, axis=1))

Four-dimension interpolant#

The \(m\)-dimensional Runge function defined above is chosen to show that interpolate() works the same way for higher-dimensional functions as it does for 1D and 2D ones.

Just make sure your function meets Minterpy’s requirements: it should be a callable that takes a 2D array as input, where each row represents a point in multidimensional space and each column corresponds to a spatial dimension (so in this case, four columns).

Just like with 2D functions, you can also tweak the \(l_p\)-degree of the underlying multi-index set for higher-dimensional functions (\(m > 1\)). This is optional, but can affect the accuracy of the interpolant.

To create a 4D interpolant with a polynomial degree of \(16\), use the following command:

interp_4d = mp.interpolate(fun_md, spatial_dimension=4, poly_degree=16)

Assessing 4D interpolant accuracy#

As before, you can use the infinity norm to gauge the accuracy of the interpolant. To estimate it using \(10'000\) random points in \([-1, 1]^4\), you can use the following code:

xx_test_4d = -1 + rng.random((10000, 4))
np.max(np.abs(fun_md(xx_test_4d) - interp_4d(xx_test_4d)))

np.float64(1.7148324011895255e-05)

For an additional cost, you can improve the accuracy of the interpolant by increasing the polynomial degree.

Summary#

Congratulations on completing this Quickstart Guide!

We hope you now know how to interpolate a function in one or multiple dimensions using Minterpy and that you find Minterpy useful for your work.

Minterpy offers more than just function approximation through interpolation. To fully appreciate its capabilities, we encourage you to explore further. We have prepared a series of tutorials designed to help you become familiar with the more advanced features of Minterpy.