Multidimensional Polynomial Interpolation#

Polynomial interpolation dates back to Newton, Lagrange, and others[1], and its fundamental importance in both mathematics and computing is widely recognized.

Interpolation is rooted in the principle that, in one dimension, there exists exactly one polynomial \(Q_{f, A}\) of degree \(n \in \mathbb{N}\) that interpolates a function \(f : \mathbb{R} \longrightarrow \mathbb{R}\) on \(n+1\) distinct interpolation nodes \(P_A = \{p_i\}_{i \in A} \subseteq \mathbb{R}\) where \(A=\{0, \ldots, n\}\). Specifically, this means

\[Q_{f,A}(p_i) = f(p_i)\,, \quad \text{for all} \quad p_i \in P_A \,, i \in A\,.\]

This makes interpolation fundamentally different from approximation, see Fig. 1.

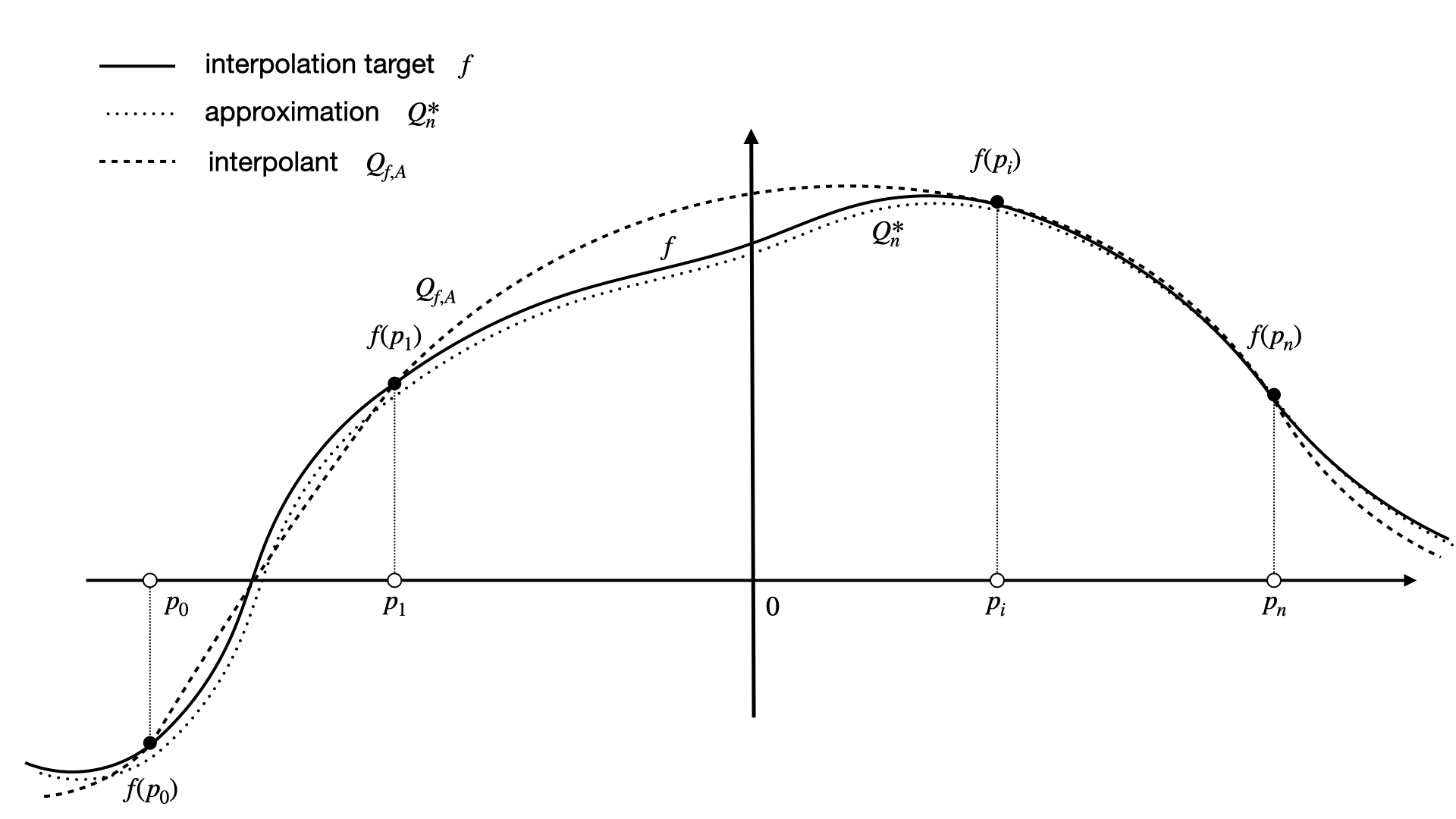
../_images/1D_interpol.png

Fig. 1 Interpolation and approximation in one dimension. While the interpolant \(Q_{f, A}\) must match the function \(f\) at the interpolation nodes \(p_0, \ldots, p_n\), an approximation \(Q^*_n\) is not required to coincide with \(f\) at all.#

Weierstrass Approximation Theorem#

The famous Weierstrass Approximation Theorem[2] asserts that any continuous function \(f : \Omega \longrightarrow \mathbb{R}\), defined on a compact domain, such as \(\Omega = [-1,1]^m\), can be uniformly approximated by polynomials[3]. However, the theorem does not require the polynomials to coincide with \(f\) at any given points. In fact, it is possible to have a sequence of multidimensional polynomials \(Q_n^*\), \(n \in \mathbb{N}\), where \(Q_n^*(x) \neq f(x)\) for all \(x \in \Omega\), but still achieve uniform approximation, that is

\[Q_{n}^* \xrightarrow[n \rightarrow \infty]{} f \quad \text{uniformly on} \quad \Omega\,.\]

There are several constructive proofs of the Weierstrass approximation theorem, including the well-known version by Serge Bernstein[4]. The resulting Bernstein approximation scheme is universal and has been shown to reach the optimal (inverse-linear) approximation rate for the absolute value function \(f(x) = |x|\) [5]. However, despite its generality, the Bernstein scheme achieves only slow convergence rates for analytic functions, leading to high computational costs in practical applications.

As a result, extensive research has focused on extending one-dimensional Newton or Lagrange interpolation schemes to multiple dimensions (mD) while preserving their computational efficiency. Any method addressing this challenge must avoid Runge’s phenomenon[6] (overfitting) by ensuring uniform approximation of the interpolation target \(f : \Omega \longrightarrow \mathbb{R}\). Additionally, it resist the curse of dimensionality, achieving highly accurate polynomial approximations for general multidimensional functions with a sub-exponential demand for data samples \(f(p)\,, p \in P_A\), where \(|P_A| \in o(n^m)\).

Lifting the curse of dimensionality#

To address the problem we consider the \(l_p\)-norm \(\|\alpha\|_p = (\alpha_1^p + \cdots +\alpha_m^p)^{1/p}\), \(\alpha = (\alpha_1,\dots,\alpha_m) \in\mathbb{N}^m\), \(m \in \mathbb{N}\) and the lexicographically-ordered and complete multi-index set

(1)#\[A_{m,n,p} = \left\{\alpha \in \mathbb{N}^m : \|\alpha\|_p \leq n \right\}\,, \quad m,n \in \mathbb{N}\,, p \geq 1\,.\]

This concept generalizes the one-dimensional notion of polynomial degree to multi-dimensional \(l_p\)-degree. Specifically, we consider the polynomial spaces spanned by all monomials with a bounded \(l_p\)-degree, that is

\[\Pi_A = \langle x^\alpha = x^{\alpha_1}\cdots x^{\alpha_m} : \alpha \in A \rangle \,, A =A_{m,n,p}\,.\]

Given \(A=A_{m,n,p}\), we ask for:

  1. Unisolvent interpolation nodes \(P_A\) that uniquely determine the interpolant \(Q_{f,A} \in \Pi_A\) by satisfying \(Q_{f,A}(p_{\alpha}) = f(p_{\alpha})\), \(\forall p_{\alpha} \in P_A\), \(\alpha \in A\).

  2. An interpolation scheme that computes the uniquely determined interpolant \(Q_{f,A} \in \Pi_A\) efficiently and with numerical accuracy (machine precision).

  3. The unisolvent nodes \(P_A\) that scale sub-exponentially with the spatial dimension \(m \in \mathbb{N}\), \(|P_A| \in o(n^m)\) and guarantee uniform approximation of even strongly varying functions (avoiding over fitting), such as as the Runge function \(f_R(x) = 1/(1+\|x\|^2)\), by achieving fast (ideally exponential) approximation rates.

In fact, the results of[7] suggest that the multidimensional DDS resolves issues 1–3 for the so called Trefethen functions by selecting the Euclidian \(l_2\)-degree and Leja ordered Chebyshev-Lobatto unisolvent interpolation nodes. Thus,

\[|P_A| \approx \frac{(n+1)^m }{\sqrt{\pi m}} (\frac{\pi \mathrm{e}}{2m})^{m/2} \in o(n^m)\,, \quad A=A_{m,n,2}\,,\]

scales sub-exponentially with space dimension \(m\) and

\[Q_{f,A_{m,n,2}} \xrightarrow[n\rightarrow \infty]{} f\]

converges uniformly and fast (exponentially) on \(\Omega = [-1,1]^m\).

Fig. 2 shows the approximation rates for the classic Runge function[6] in dimension \(m = 4\), which is known to exhibit Runge’s phenomenon (over-fitting) when interpolated naively.

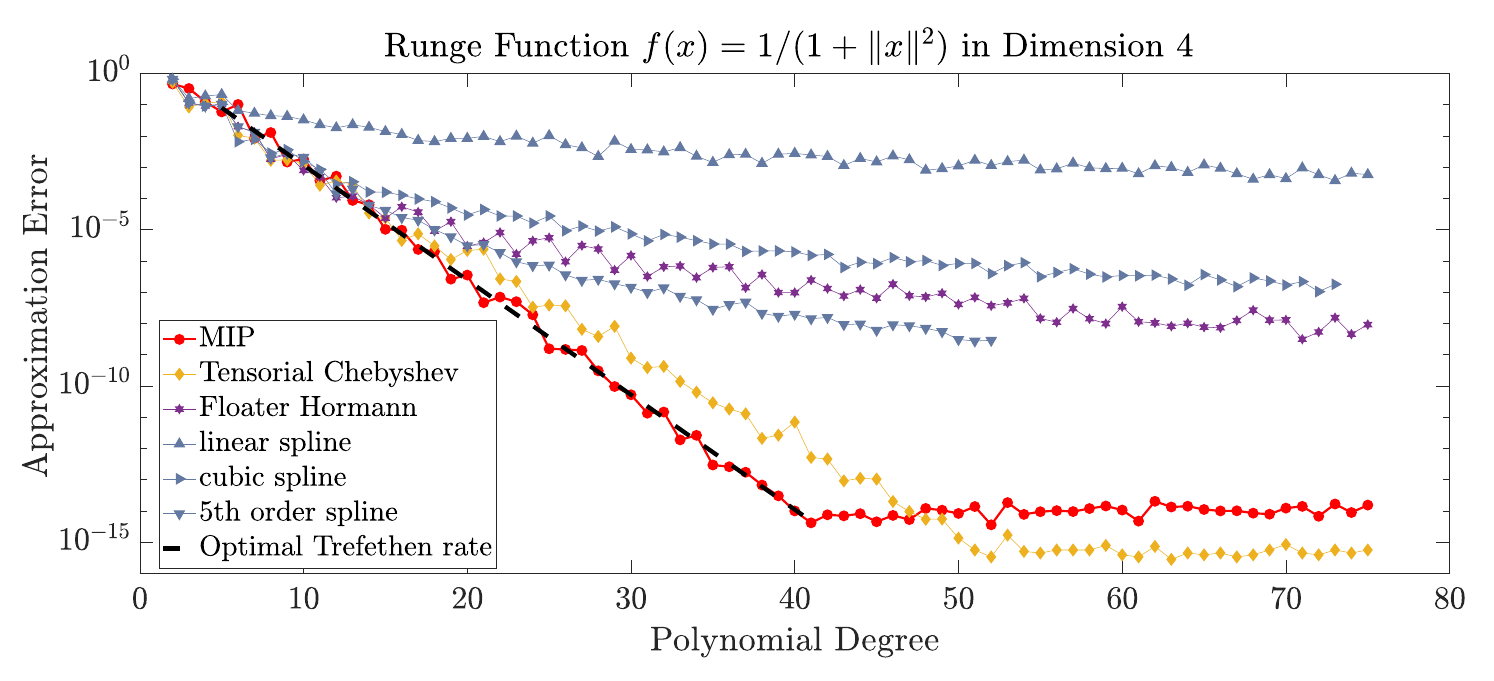
../_images/mip_approximation.png

Fig. 2 Approximation errors rates for interpolating the Runge function in dimension \(m = 4\).#

There is an optimal (upper bound) approximation rate

\[\|Q_{f,A} - f\| \in \mathcal{O}_{\varepsilon}(\rho^{-n})\]

known[8], which we call the Trefethen rate.

In fact, the the DDS scheme numerically reaches the optimal Trefethen rate. In contrast, spline-type interpolation is based on works of Carl de Boor et al.[9][10][11][12] and limited to reach only polynomial approximation rates[13]. Similarly, interpolation using rational functions, such as Floater-Hormann interpolation[14][15] and tensorial Chebyshev interpolation, relying on \(l_{\infty}\)-degree[16], do not achieve optimality.

By combining sub-exponential growth of node (data) counts with exponential approximation rates, the DDS algorithm has the potential to lift the curse of dimensionality for interpolation problems involving regular (Trefethen) functions[7].

References